Số nguyên là gì? Số thực là gì? Cách phân biệt Số nguyên với Số thực?

Số nguyên và Số thực đều là những định nghĩa cơ bạn dạng được dùng vô Toán học tập. Và cả vô ngôi trường học tập lẫn lộn cuộc sống, Toán học tập vẫn là một cỗ môn sở hữu lượng kỹ năng đa dạng và phong phú và vô tận, thú vị thật nhiều sự quan hoài của toàn bộ từng người! Qua nội dung bài viết này, tôi sẽ giúp cho bạn nói lại một trong những kỹ năng như: Số vẹn toàn là gì? Số thực là gì? Cách phân biệt Số vẹn toàn với Số thực?

1.1. Định nghĩa của Số nguyên

Trong Toán học tập, Số nguyên bao bao gồm các Số vẹn toàn dương, Số vẹn toàn âm và Số 0. Hay còn thưa cách tiếp, Số nguyên là tập kết bao gồm Số 0, Số đương nhiên dương và Số đương nhiên âm (các số đối của số đương nhiên dương). Tập ăn ý của Số nguyên là vô hạn, tuy nhiên hoàn toàn có thể điểm được (ký hiệu là Z).

Bạn đang xem: Số nguyên là gì? Số thực là gì? Cách phân biệt Số nguyên với Số thực?

1.2. Phân loại của Số nguyên

Số nguyên được chia thành 2 loại là Số vẹn toàn âm và Số vẹn toàn dương.

1.2.1. Số vẹn toàn dương là gì?

Ta hoàn toàn có thể hiểu Số vẹn toàn dương là những Số nguyên lớn rộng lớn 0, và sở hữu ký hiệu là Z+.

Ví dụ: 1, 2, 3, 4, 5, 6,…

1.2.2. Số vẹn toàn âm là gì?

Còn Số vẹn toàn âm gồm tập kết những số đối của Số vẹn toàn dương, là các Số nguyên nhỏ rộng lớn 0, và sở hữu ký hiệu là Z-.

Ví dụ: -1, -2, -3, -4, -5,…

Xem thêm: CÁC BIỆN PHÁP TU TỪ: SO SÁNH, NHÂN HÓA, ĐIỆP NGỮ I Lý thuyết

1.2.3. Số 0

Số 0 cũng là một trong những phần của Số nguyên, tuy nhiên nó ko thuộc Số vẹn toàn dương cũng như Số vẹn toàn âm.

1.3. Tính hóa học của Số nguyên

Số nguyên có 4 đặc thù cơ bạn dạng, bao gồm:

1. Không sở hữu số vẹn toàn này là lớn số 1 và không tồn tại số vẹn toàn này nhỏ nhất.
2. Số vẹn toàn dương nhỏ nhất là một trong và số vẹn toàn âm lớn số 1 là -1.
3. Số vẹn toàn Z sở hữu tập kết con cái hữu hạn luôn luôn sở hữu thành phần lớn số 1 và thành phần nhỏ nhất.
4. Không sở hữu số vẹn toàn này nằm trong lòng nhì số vẹn toàn liên tục.

2. Số thực là gì?

2.1. Định nghĩa của Số thực

Số thực là một tập kết bao hàm số dương, số 0, số âm số hữu tỉ, số vô tỉ. Vậy tức là Số nguyên là tập kết con cái của Số thực. Số thực được màn trình diễn bên trên một trục số lâu năm vô hạn (Ký hiệu là R).

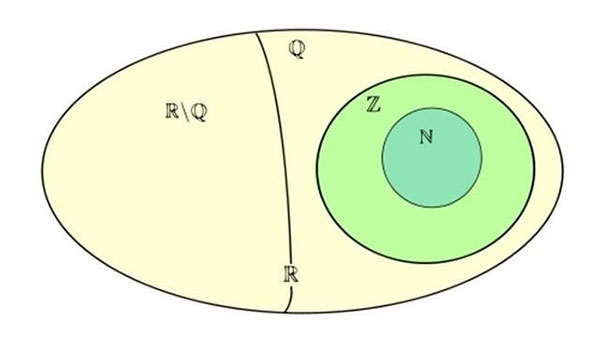
Chú mến hình màn trình diễn tập luyện hợp Số thực:

Xem thêm: Chất nào sau đây là hợp chất hữu cơ? A. HCOONa. B. (NH4)2CO3. C. NaHCO3. D. CaC2. (Miễn phí)

• N: Tập ăn ý Số đương nhiên.
• Z: Tập hợp Số nguyên.
• Q: Tập ăn ý Số hữu tỉ.
• I = RQ: Tập ăn ý Số vô tỉ.

2.2. Tính hóa học của Số thực

Số thực được kiến thiết dựa vào những đặc thù của những số tạo thành nó như: Số nguyên, Số vô tỉ, Số hữu tỉ…

3. Cách phân biệt Số vẹn toàn với Số thực?

Để phân biệt Số nguyên với Số thực, tất cả chúng ta cần thiết lưu ý 3 Điểm lưu ý cần thiết sau:

• Số nguyên chỉ là tập luyện con cái của Số thực.
• Số nguyên là tập kết những số điểm được.
• Số thực là tập kết những số ko điểm được.

Hy vọng qua quýt những vấn đề này cung cung cấp vô nội dung bài viết bên trên sẽ hỗ trợ cho tới chúng ta cầm rõ Số vẹn toàn là gì? Số thực là gì? Cách phân biệt Số vẹn toàn với Số thực? Rất cảm ơn chúng ta đang được theo gót dõi nội dung này. Nếu các bạn sở hữu những thắc mắc khác? Vui lòng nhằm lại ở bên dưới phần comment. Xin cảm ơn!