Bài tập luyện Toán 9: Chứng minh tía điểm trực tiếp hàng là một dạng toán hình xuất hiện tại nhiều nhập đề đua tuyển chọn sinh nhập lớp 10 môn Toán. Tài liệu được GiaiToan.com biên soạn và reviews cho tới chúng ta học viên nằm trong quý thầy cô tìm hiểu thêm. Nội dung tư liệu sẽ hỗ trợ chúng ta học viên học tập chất lượng tốt môn Toán lớp 9 hiệu suất cao rộng lớn. Mời chúng ta tìm hiểu thêm.
A. Cách chứng minh ba điểm thẳng hàng
Cách 1: Sử dụng nhị góc kề bù với tía điểm phía trên nhị cạnh là nhị tia đối nhau.
Bạn đang xem: Chứng minh 3 điểm thẳng hàng
Cách 2: Hai đường thẳng liền mạch nằm trong trải qua nhị nhập tía điểm ấy nằm trong vuông góc với đường thẳng liền mạch loại ba
Cách 3: Hai đường thẳng liền mạch nằm trong trải qua nhị nhập tía điểm ấy nằm trong tuy vậy song với đường thẳng liền mạch loại ba
Cách 4: Sử dụng đặc điểm lối phân giác của một góc, đặc điểm lối trung trực của đoạn trực tiếp, đặc điểm tía lối cao của tam giác.
B. Bài tập luyện chứng minh ba điểm thẳng hàng
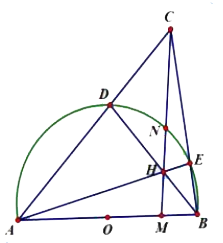
Ví dụ 1: Cho nửa lối đường kính trắng tròn trặn (O; R), 2 lần bán kính AB. Một điểm M thắt chặt và cố định nằm trong đoạn trực tiếp OB (M không giống B và M không giống O). Đường trực tiếp d vuông góc với AB bên trên M rời nửa lối tròn trặn vẫn mang đến bên trên N. Trên cung NB lấy điểm E bất kì (E không giống B và E không giống N). Tia BE rời đường thẳng liền mạch d bên trên C, đường thẳng liền mạch AC rời nửa lối tròn trặn bên trên D. Gọi H là giao phó điểm của AE và đường thẳng liền mạch d.
a) Chứng minh tứ giác BMHE nội tiếp lối tròn trặn.
b) Chứng minh tía điểm B, D, H trực tiếp mặt hàng.
Hướng dẫn giải
Hình vẽ minh họa
a) Ta có: 
(giả thiết)
(góc nột tiếp chắn nửa lối tròn)
Xét tứ giác HEBM tớ với ở địa điểm đối nhau và
Vậy tứ giác HEBM nội tiếp lối tròn trặn.
b) Xét tam giác CAB với AE ⊥ CB nên AE là lối cao nhập tam giác CAB.
CA ⊥ BD (góc nội tiếp chắn nửa lối tròn)
=> BD là lối cao nhập tam giác CAB
Ta với BD giao phó với AE bên trên H nên H là trực tâm của tam giác CAB.
Vậy B, H, D trực tiếp mặt hàng.
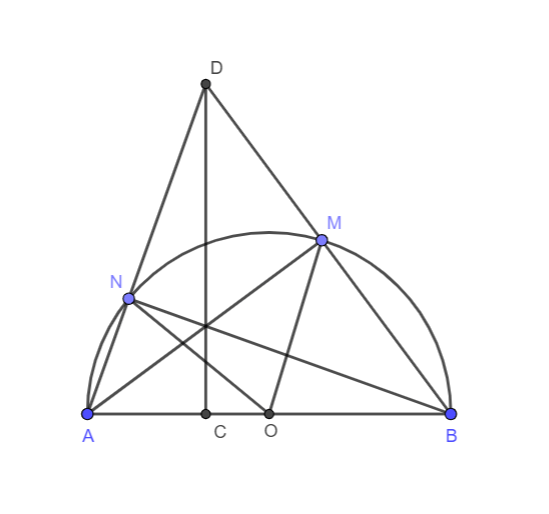
Ví dụ 2: Cho nửa lối tròn trặn tâm O, 2 lần bán kính AB. Lấy điểm C bên trên đoạn trực tiếp OA (C không giống O và C không giống A). Đường trực tiếp trải qua C và vuông góc với AB rời nửa lối tròn trặn bên trên K. Gọi M là vấn đề bất kì bên trên cung BK (M không giống B và K). Đường trực tiếp CK rời những đường thẳng liền mạch AM, BM thứu tự bên trên H và D. Đường trực tiếp BH rời nửa lối tròn trặn bên trên điểm loại nhị là N. Chứng minh tía điểm A, N, D trực tiếp mặt hàng và tiếp tuyến bên trên N của nửa lối tròn trặn trải qua trung điểm của HD.
Hướng dẫn giải
Hình vẽ minh họa:
Xem thêm: Dãy Hoạt Động Hóa Học Của Kim Loại: Tính Chất Và Cách Để Nhớ Nhanh
a) Chứng minh AN ⊥ BN kể từ fake thiết N ∈ (O) 2 lần bán kính AB.
Chứng minh AD ⊥ BN:
Chỉ rời khỏi AM, DC là hai tuyến đường cao của tam giác ABD, AM ∩ DC = {H} nên H là trực tâm của tam giác ABD
=> AD ⊥ BH hoặc AD ⊥ BN
=> Ba điểm A, N, D trực tiếp mặt hàng.
b) Gọi I là trung điểm cuả DH. Chỉ rời khỏi tam giác DHN vuông bên trên N là với NI là trung tuyến
=> NI = DH/2 = DI (tính hóa học trung tuyến của tam giác vuông)
=> Tam giác IDN cân nặng bên trên I =>
Chỉ rời khỏi tam giác OAN cân nặng bên trên O =>
=>
Xét tam giác ACD vuông bên trên C nên
=> IN ⊥ ON
Mà ON là nửa đường kính của (O) nên IN là tiếp tuyến của (O) hoặc tiếp tuyến N của (O) trải qua I là trung điểm của DH.
C. Bài tập luyện tự động luyện chứng minh ba điểm thẳng hàng
Bài tập luyện 1: Cho tam giác ABC vuông bên trên A. Đường tròn trặn 2 lần bán kính AB rời BC bên trên D không giống B. Gọi M là vấn đề bất kì bên trên đoạn AD. Kẻ MH, XiaoMi MI thứu tự vuông góc với AB, AC bên trên H, I. Kẻ HK vuông góc với ID bên trên K. Chứng minh và tứ giác AIKM nội tiếp, kể từ bại liệt minh chứng tía điểm K, M, B trực tiếp mặt hàng.
Bài tập luyện 2: Cho tam giác ABC vuông bên trên A. Lấy B thực hiện tâm, vẽ lối tròn trặn nửa đường kính BA, lấy điểm C thực hiện tâm, vẽ lối tròn trặn nửa đường kính AC. Hai lối tròn trặn này rời nhau bên trên điểm loại nhị là D. Vẽ AM và AN thứu tự là những chão cung của lối tròn trặn (B) và (C) sao mang đến AM vuông góc với AN và D nằm trong lòng M và N. Chứng minh tía điểm M, D, N trực tiếp mặt hàng.
Bài tập luyện 3: Cho nửa lối tròn trặn (O; R) 2 lần bán kính AB. Gọi C là vấn đề bất kì nằm trong nửa lối tròn trặn sao mang đến 0 < AC < BC. Gọi D là vấn đề nằm trong cung nhỏ BC sao mang đến . Gọi E là giao phó điểm của AD và BC, F là giao phó điểm của AC và BD. Gọi I la trung điểm của EF. Chứng minh IC là tiếp tuyến của (O).
Bài tập luyện 4: Cho hình thang ABCD với AB//CD. Gọi O là giao phó điểm của hai tuyến đường chéo cánh AC và
BD. Gọi M, N, Phường thứu tự là trung điểm của AB, BC, AD. Gọi E là trung điểm của PN.
Chứng minh rằng tía điểm M, O, E trực tiếp mặt hàng.
Bài tập luyện 5: Cho tam giác ABC nhọn nội tiếp lối tròn trặn (O). Điểm M ngẫu nhiên bên trên cung nhỏ
BC. Gọi E, F trật tự là những điểm đối xứng của M qua quýt AB, AC. Gọi H là trực tâm tam giác
ABC. Chứng minh rằng E, H, F trực tiếp mặt hàng.
-------------------------------------
Xem thêm: Vật lí 11, giải lí 11 chân trời sáng tạo
Hy vọng tư liệu Chứng minh tía điểm trực tiếp mặt hàng sẽ mang lại lợi ích mang đến chúng ta học viên học tập tóm kiên cố kỹ năng chuyên mục Đường tròn trặn mặt khác học tập chất lượng tốt môn Toán lớp 9. Chúc chúng ta học tập chất lượng tốt, chào chúng ta tham lam khảo!
Ngoài rời khỏi chào quý thầy cô và học viên tìm hiểu thêm tăng một số trong những nội dung:
- Luyện tập luyện Toán 9
- Giải bài bác tập luyện SGK Toán 9
- Đề đua thân mật học tập kì môn Toán 9
Câu căn vặn không ngừng mở rộng gia tăng con kiến thức:
- Cho tam giác ABC nội tiếp lối tròn trặn (C) và tia phân giác của góc A rời lối tròn trặn bên trên M. Vẽ lối cao AH
- Từ điểm M ở phía bên ngoài lối tròn trặn (O; R) vẽ nhị tiếp tuyến MA, MB của (O) (với A, B là những tiếp điểm) và cát tuyến MDE ko qua quýt tâm O (D, E nằm trong (O), D nằm trong lòng M và E).
- Một xe cộ máy lên đường kể từ A cho tới B với véc tơ vận tốc tức thời và thời hạn dự trù trước. Sau Khi lên đường được nửa quãng lối, xe cộ máy gia tăng 10km/h chính vì vậy xe cộ máy cho tới B sớm rộng lớn nửa tiếng đối với ý định. Tính véc tơ vận tốc tức thời ý định của xe cộ máy, biết quãng lối AB nhiều năm 120km.
- Tìm nhị số đương nhiên hiểu được tổng của bọn chúng vị 1006 và nếu như lấy số rộng lớn phân tách mang đến số nhỏ thì được thương là 2 và số dư là 124
- Một ôtô lên đường kể từ A và ý định cho tới B khi 12 giờ trưa. Nếu xe đua với véc tơ vận tốc tức thời 35km/h thì sẽ tới B chậm trễ 2 tiếng đồng hồ đối với quy lăm le. Nếu xe đua với véc tơ vận tốc tức thời 50km/h thì sẽ tới B sớm 1 giờ đối với ý định. Tính phỏng nhiều năm quãng lối AB và thời gian xuất trừng trị của siêu xe bên trên A.
- Giải việc cổ sau Quýt, cam chục bảy trái ngược tươi tắn Đem phân tách cho 1 trăm con người nằm trong vui
- Giải việc bằng phương pháp lập hệ phương trình dạng gửi động
- Một quần thể vườn hình chữ nhật với chu vi 280m. Người tớ thực hiện 1 lối lên đường xung xung quanh vườn ( nằm trong khu đất của vườn) rộng lớn 2m. Diện tích còn sót lại nhằm trồng trọt là 4256m2 . Tìm diện tích S vườn khi đầu.
- Hai xe hơi lên đường ngược hướng kể từ A cho tới B, xuất trừng trị ko nằm trong lúc
- Cho tam giác ABC vuông bên trên A. bên trên AC lấy một điểm M và vẽ lối tròn trặn 2 lần bán kính MC. Kẻ BM rời lối tròn trặn bên trên D. Đường trực tiếp DA rời lối tròn trặn bên trên S. Chứng minh rằng:a. ABCD là 1 tứ giác nội tiếpb. c. CA là tia phân giác của góc SCB.
- Cho nửa lối tròn trặn tâm O 2 lần bán kính AB, C là 1 điểm nằm trong lòng O và A. Đường trực tiếp vuông góc với AB bên trên C rời nửa lối tròn trặn bên trên trên I, K là 1 điểm ở bất kì bên trên đoạn trực tiếp CI (K không giống C và I) tia AK rời nửa lối tròn trặn O bên trên M tia BM rời tia CI bên trên D.Chứng minh:a) Các tứ giác ACMD, BCKM nội tiếp lối trònb) CK.CD = CA.CBc) Gọi N là giao phó điểm của AD và lối tròn trặn O minh chứng B, K, N trực tiếp hàngd) Tâm lối tròn trặn nước ngoài tiếp tam giác AKD phía trên một đường thẳng liền mạch thắt chặt và cố định Khi K địa hình bên trên đoạn trực tiếp CI
Bình luận