Chủ đề Cách vẽ hình tứ diện đều: Vẽ hình tứ diện đều là một kỹ năng cần thiết cho bất kỳ ai quan tâm đến hình học không gian. Bài viết này sẽ cung cấp hướng dẫn từng bước cụ thể, giúp bạn dễ dàng hình dung và thực hiện vẽ một tứ diện đều chỉ với vài công cụ đơn giản.
Mục lục
- Cách Vẽ Hình Tứ Diện Đều
- Giới thiệu về hình tứ diện đều
- Các bước cơ bản để vẽ hình tứ diện đều
- Công cụ và nguyên liệu cần thiết
- Lưu ý khi vẽ hình tứ diện đều
- Ứng dụng thực tế của hình tứ diện đều
- Các vấn đề thường gặp và cách khắc phục
- Hỏi đáp - Câu hỏi thường gặp
- Kết luận và lời khuyên
- YOUTUBE: HÌNH KG 11: HÌNH CHÓP ĐỀU - TỨ DIỆN ĐỀU
Cách Vẽ Hình Tứ Diện Đều
Tứ diện đều là một khối đa diện quan trọng trong toán học và hình học. Việc vẽ tứ diện đều không chỉ giúp hiểu rõ hơn về cấu trúc của nó mà còn hỗ trợ giải quyết các bài toán liên quan. Dưới đây là các bước vẽ một tứ diện đều:
- Bước 1: Vẽ một hình vuông.
- Bước 2: Vẽ đường chéo của hình vuông để tạo thành hai tam giác đều.
- Bước 3: Kết nối hai đỉnh nằm giữa hai tam giác để tạo thành một đường thẳng, đây là đường cao của tứ diện đều.
- Bước 4: Vẽ tiếp một hình vuông khác, có cạnh vuông góc với hình vuông ban đầu và cách xa hình vuông ban đầu một khoảng bằng với độ dài đường cao của tứ diện.
- Bước 5: Vẽ các cạnh nối giữa các đỉnh của hai hình vuông đã vẽ để tạo thành tứ diện đều.
Các cạnh của tứ diện đều có cùng chiều dài và các góc giữa các cạnh là góc vuông. Để vẽ chính xác, việc sử dụng phần mềm hỗ trợ đồ họa có thể giúp giảm thiểu sai sót.
Ứng Dụng Của Tứ Diện Đều
Tứ diện đều không chỉ có giá trị trong học thuật mà còn được ứng dụng trong thực tế, ví dụ như trong thiết kế các món đồ chơi, vật dụng trang trí, và nhiều ứng dụng khác trong kiến trúc và thiết kế công nghiệp.
Các Tính Chất Của Tứ Diện Đều
- Mỗi mặt của tứ diện đều là một tam giác đều.
- Tất cả các góc trong tứ diện đều là góc nhọn.
- Mỗi đỉnh của tứ diện là điểm gặp của ba cạnh và ba góc bằng nhau.

Giới thiệu về hình tứ diện đều
Hình tứ diện đều là một trong những dạng hình học cơ bản và quan trọng, được sử dụng rộng rãi trong nhiều bài toán hình học không gian. Đây là khối đa diện lồi đơn giản nhất, gồm bốn mặt tam giác đều, sáu cạnh và bốn đỉnh.
- Mỗi mặt của tứ diện là một tam giác đều.
- Tất cả các cạnh của tứ diện đều có cùng độ dài.
- Góc tạo bởi bất kỳ hai mặt tam giác đều của tứ diện là như nhau và đều là góc nhọn.
Đây là dạng hình đa diện duy nhất có số mặt ít hơn năm, mỗi mặt đều là một tam giác, tạo nên một cấu trúc vô cùng đặc biệt và hấp dẫn trong thế giới hình học.
Các bước cơ bản để vẽ hình tứ diện đều
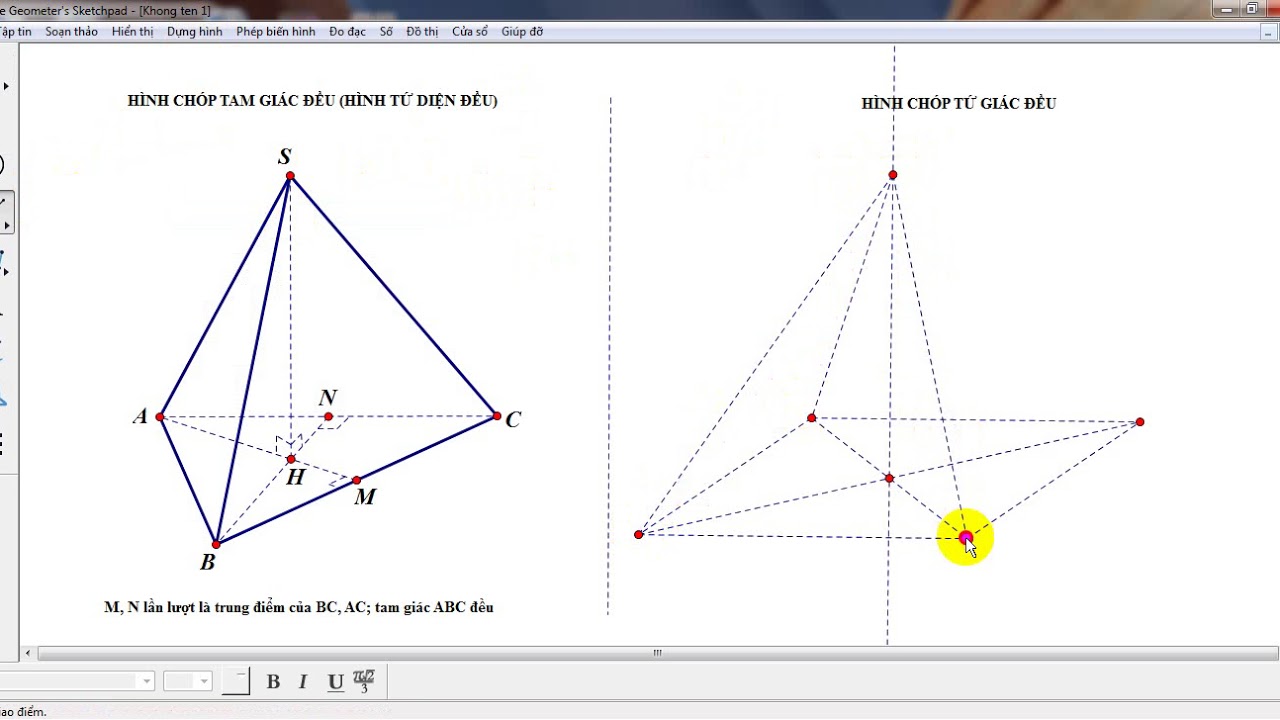
Vẽ một hình tam giác đều làm mặt đáy. Trong hướng dẫn này, tam giác này sẽ được gọi là tam giác BCD.
Trong tam giác BCD, kẻ một đường trung tuyến từ đỉnh B đến trung điểm M của cạnh CD, đường này gọi là BM.
Xác định trọng tâm G của tam giác BCD trên đường trung tuyến BM sao cho khoảng cách BG gấp đôi GM.
Dựng đường cao từ trọng tâm G đi lên. Đỉnh A của hình tứ diện sẽ nằm trên đường này và cao hơn trọng tâm.
Nối đỉnh A với các đỉnh B, C, D để tạo thành ba cạnh bên của tứ diện đều.
Hoàn thành các bước trên, bạn sẽ có một hình tứ diện đều với các thành phần sau:
- 4 đỉnh: A, B, C, D
- 6 cạnh: AB, AC, AD, BC, CD, BD
- 4 mặt: tam giác ABC, ACD, ABD, BCD
Đây là một phương pháp đơn giản để vẽ hình tứ diện đều mà bạn có thể thực hiện chỉ với giấy và bút chì.
XEM THÊM:
- Hình Tứ Diện Đều ABCD: Khám Phá Cấu Trúc Và Công Thức Tính
- Cách Làm Hình Tứ Diện Đều Bằng Giấy: Bí Quyết và Hướng Dẫn Chi Tiết
Công cụ và nguyên liệu cần thiết
Để vẽ hình tứ diện đều, bạn sẽ cần những công cụ và nguyên liệu sau:
- Bút chì: Dùng để vẽ bản phác thảo ban đầu.
- Thước kẻ: Cần thiết để đo và vẽ các đoạn thẳng chính xác.
- Compa: Dùng để vẽ các đường tròn hoặc cung cần thiết cho các cạnh bằng nhau.
- Giấy vẽ: Nên sử dụng giấy có định lượng phù hợp để bản vẽ được nét và dễ dàng chỉnh sửa.
- Eraser (tẩy): Để xóa những nét vẽ sai.
Ngoài ra, nếu bạn muốn hình vẽ có độ chính xác cao hoặc muốn thử nghiệm với phần mềm, có thể sử dụng:
- Phần mềm đồ họa: Như AutoCAD, SketchUp hoặc GeoGebra để vẽ và xem mô hình 3D trực quan.
- Máy in 3D: Để tạo mô hình vật lý từ bản vẽ số, giúp dễ dàng hình dung và kiểm tra mô hình.
Các nguyên liệu và công cụ này giúp bạn dễ dàng thực hiện bản vẽ tứ diện đều từ bước đầu tiên đến khi hoàn thành.

Lưu ý khi vẽ hình tứ diện đều
Khi vẽ hình tứ diện đều, một số điểm lưu ý quan trọng sẽ giúp bạn đạt được kết quả chính xác và cân đối:
- Đảm bảo rằng tất cả các cạnh của tứ diện đều có độ dài bằng nhau, điều này là cốt lõi để duy trì sự đều đặn của hình.
- Tất cả các mặt của tứ diện phải là các tam giác đều, và mỗi góc trong các tam giác này phải là 60 độ.
- Sử dụng đường trung tuyến và đường cao một cách chính xác trong các bước vẽ để định hình các mặt và đỉnh của tứ diện.
- Trong trường hợp vẽ bằng phần mềm đồ họa, hãy kiểm tra tính năng hiển thị 3D để có cái nhìn tổng thể về hình dạng và sự cân bằng của tứ diện.
- Khi dựng tứ diện đều, xác định trọng tâm của tam giác đáy và dựng đường cao từ trọng tâm này lên đỉnh tứ diện, đây là bước quan trọng để đảm bảo tính chính xác.
Ngoài ra, sự chính xác trong việc kết nối các đỉnh với nhau là yếu tố không thể thiếu để hình tứ diện đều được hoàn thiện một cách hoàn hảo.
Ứng dụng thực tế của hình tứ diện đều
Hình tứ diện đều không chỉ là một đối tượng nghiên cứu trong toán học và kiến trúc mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực khác nhau:
- Kiến trúc và xây dựng: Tứ diện đều được sử dụng trong thiết kế kiến trúc, từ cơ bản như móng cọc cho đến phức tạp như thiết kế mái nhà, giúp tính toán độ ổn định và thẩm mỹ.
- Khoa học và kỹ thuật: Trong các bài toán liên quan đến cơ học và kỹ thuật, hình tứ diện đều giúp mô hình hóa và phân tích các cấu trúc phức tạp.
- Đóng gói và vận chuyển: Tứ diện đều cũng được ứng dụng trong thiết kế bao bì để tối ưu hóa không gian lưu trữ và vận chuyển, nhờ vào hình dạng độc đáo và khả năng chứa đựng hiệu quả.
- Nghệ thuật và trang trí: Nhờ vào tính thẩm mỹ cao, tứ diện đều được sử dụng trong nghệ thuật tạo hình, trang trí nội thất và thiết kế đồ trang sức.
- Giáo dục và nghiên cứu: Tứ diện đều là một mô hình hình học giúp sinh viên và nhà nghiên cứu dễ dàng hình dung các khái niệm trong không gian ba chiều.
Các ứng dụng của hình tứ diện đều chứng tỏ sự linh hoạt và hiệu quả của nó trong nhiều ngành nghề và bối cảnh khác nhau, từ thực tiễn đến lý thuyết.
XEM THÊM:
- Cách Gấp Hình Tứ Diện Đều: Bí Quyết và Kỹ Thuật Đơn Giản
- Số Mặt Phẳng Đối Xứng của Hình Tứ Diện Đều: Khám Phá Bí Ẩn Hình Học
Các vấn đề thường gặp và cách khắc phục
Khi vẽ hình tứ diện đều, người học có thể gặp một số vấn đề thường gặp sau đây và đây là cách để khắc phục chúng:
- Sai lệch tỷ lệ: Đôi khi các cạnh của tứ diện không đều nhau do sai lệch trong việc đo hoặc vẽ. Để khắc phục, hãy sử dụng compa và thước kẻ để đảm bảo tính chính xác trong từng bước.
- Vị trí đỉnh không chính xác: Việc định vị sai vị trí của đỉnh có thể làm hỏng hình dạng tứ diện. Hãy sử dụng công cụ trực tuyến hoặc phần mềm CAD để xác định chính xác vị trí đỉnh dựa trên các tính toán hình học.
- Khó khăn trong việc tạo mặt phẳng đáy: Nếu khó khăn trong việc vẽ mặt đáy, hãy bắt đầu với một tam giác đều rõ ràng và đảm bảo rằng tất cả các góc và cạnh được xác định chính xác trước khi tiếp tục.
- Dựng đường cao không chính xác: Đường cao phải thực sự vuông góc với mặt đáy và đi qua trọng tâm của tam giác. Sử dụng công thức hình học để kiểm tra và điều chỉnh độ dài và hướng của đường cao.
Việc chú ý đến các chi tiết nhỏ và kiểm tra lại từng bước trong quá trình vẽ có thể giúp giảm thiểu sai sót và cải thiện chất lượng của hình tứ diện đều cuối cùng.
Hỏi đáp - Câu hỏi thường gặp
Dưới đây là một số câu hỏi thường gặp liên quan đến vẽ hình tứ diện đều và các giải đáp của chúng:
- Câu hỏi: Làm thế nào để xác định trọng tâm của tứ diện đều?
Trả lời: Trọng tâm của tứ diện đều nằm tại điểm giao của các đường thẳng nối từ đỉnh tới trung điểm của cạnh đối diện đáy. Trong hình tứ diện đều, trọng tâm này cũng là tâm của khối tứ diện.
- Câu hỏi: Cách vẽ tứ diện đều bắt đầu như thế nào?
Trả lời: Bắt đầu bằng cách vẽ một tam giác đều, xác định trọng tâm của tam giác này, sau đó vẽ đường cao từ trọng tâm đến điểm trên cao sao cho tạo thành một đỉnh mới. Kết nối điểm này với ba đỉnh của tam giác đáy để hoàn thành tứ diện.
- Câu hỏi: Tứ diện đều có bao nhiêu mặt phẳng đối xứng?
Trả lời: Tứ diện đều có sáu mặt phẳng đối xứng, mỗi mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện của nó.
- Câu hỏi: Số đỉnh của tứ diện đều là bao nhiêu?
Trả lời: Tứ diện đều có bốn đỉnh, và mỗi đỉnh được nối với ba đỉnh còn lại bằng các cạnh có độ dài bằng nhau.
- Câu hỏi: Có bao nhiêu cạnh trong một tứ diện đều?
Trả lời: Tứ diện đều có sáu cạnh, và tất cả các cạnh này có độ dài bằng nhau.
Kết luận và lời khuyên
Khi vẽ hình tứ diện đều, việc hiểu rõ cấu trúc và các thuộc tính của nó là rất quan trọng. Dưới đây là một số kết luận và lời khuyên để giúp bạn cải thiện kỹ năng vẽ và hiểu sâu hơn về hình tứ diện đều:
- Thực hành thường xuyên: Càng thực hành nhiều, bạn càng có khả năng vẽ chính xác hơn. Hãy bắt đầu với các bản phác thảo đơn giản và từ từ tăng độ phức tạp.
- Sử dụng công cụ hỗ trợ: Để đạt độ chính xác cao, bạn có thể sử dụng các phần mềm đồ họa máy tính như AutoCAD hoặc GeoGebra, điều này giúp bạn kiểm tra và chỉnh sửa mô hình dễ dàng.
- Hiểu rõ các thuộc tính: Tứ diện đều có các mặt là tam giác đều, các cạnh bằng nhau và các góc bằng nhau. Điều này cần được xem xét khi xác định các đỉnh và cạnh trong quá trình vẽ.
- Chú ý đến đường cao: Đường cao trong tứ diện đều là một yếu tố quan trọng giúp định hình cấu trúc của nó. Đảm bảo rằng đường cao được vẽ chính xác từ trọng tâm của tam giác đáy lên đỉnh tứ diện.
- Luyện tập giải các bài toán: Thực hành giải các bài toán liên quan đến tứ diện đều để nâng cao kỹ năng và hiểu biết về hình học không gian.
Cuối cùng, hãy kiên nhẫn và cẩn thận trong từng bước vẽ để đảm bảo rằng mọi chi tiết đều chính xác và tỉ mỉ. Việc nắm vững cách vẽ hình tứ diện đều sẽ mở ra nhiều cơ hội học tập và ứng dụng trong nhiều lĩnh vực khác nhau của toán học và thiết kế.
XEM THÊM:
- Hình Tứ Diện: Khám Phá Cấu Trúc và Ứng Dụng Thú Vị
- Chia hình lập phương thành 5 tứ diện: Một phương pháp hình học đột phá
HÌNH KG 11: HÌNH CHÓP ĐỀU - TỨ DIỆN ĐỀU
[Geogebra] Vẽ tứ diện đều
TOÁN LỚP 11 - MẸO, KĨ NĂNG VÀ QUY TẮC VẼ HÌNH HỌC KHÔNG GIAN SIÊU NHANH, HÌNH ĐẸP VÀ CHUẨN
XEM THÊM:
- "Tính hình tứ giác": Khám phá Tất Tần Tật về Các Dạng Tứ Giác và Ứng Dụng Thực Tiễn
- Số cạnh của một hình tứ diện là: Khám phá hình học độc đáo và ứng dụng